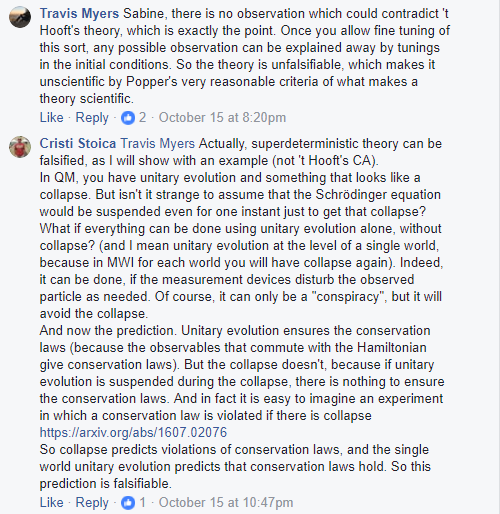
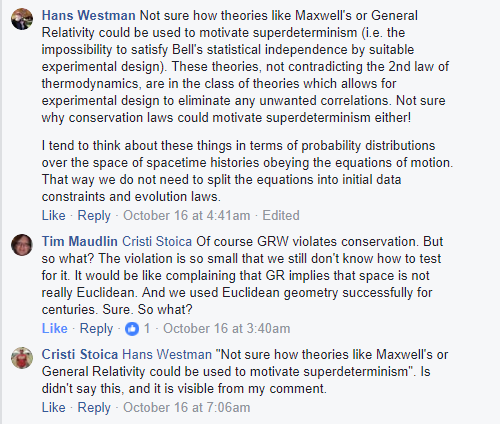
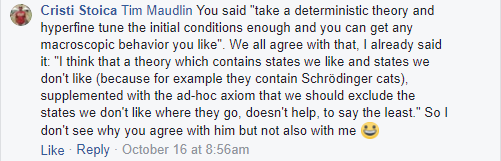
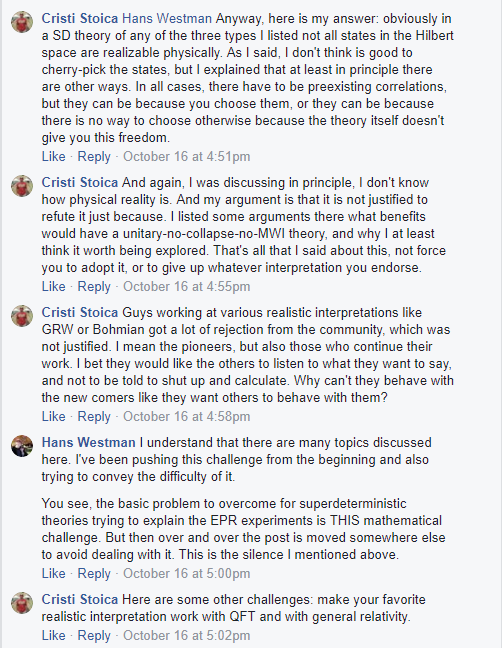
Tim Maudlin debated Gerard 't Hooft about his cellular automaton interpretation of quantum mechanics in a series of Facebook posts, the fourth one being here https://www.facebook.com/tim.maudlin/posts/10155699914028398. Somewhere in the forest of comments I was engaged in a sort of sub-debate, with Tim, Hans, and others. Sabine was there too. The discussion was completely surrealistic, Tim and Hans completely misunderstood my point. This started by me intervening with a theoretical counterexample to a claim that all so called superdeterministic theories (in particular 't Hooft's) are not falsifiable, and of course it led to different topics. It is not known, but not a secret that the wavefunction collapse leads to violations of conservation laws, and that it is possible at least in principle to remove the collapse while remaining with a single world. But removing the collapse can be seen as superdeterministic (although I wouldn't call it like this, because it is based on spacetime, not on initial conditions), and I even proposed a principle to explain this, and experiments to test it. I paste here most of this *debate*, because there are some parts I am interested to keep. I skipped some parts in which I was not involved.
Friday, October 20, 2017
Thursday, May 11, 2017
Maudlin's "(Information) Paradox Lost" paper
Tim Maudlin has an interesting paper in which he criticizes the importance given to the black hole information paradox, and even brings arguments that it is not even a problem: (Information) Paradox Lost. I agree that the importance of the problem is perhaps exaggerated, but at the same time many consider it to be a useful benchmark to test quantum gravity solutions. This led to decades of research made by many physicists, and to many controversies. I wrote a bit about some of the proposed solutions to the problem in some older posts, for example [1,2,3]. Maudlin's paper is discussed by Sabine here.
One of the central arguments in Maudlin's paper is that the well-known spacetime illustrating the information loss can be foliated into some 3D spaces (which are Cauchy hypersurfaces that are discontinuous at the singularity). These hypersurfaces have a part outside the black hole, and another one inside it, which are not connected to one another. Cauchy hypersurfaces contain the Cauchy data necessary to solve the partial differential equations, so the information should be preserved if we consider both their part inside and their part outside the black hole.
I illustrate this with this animated gif:
I made this gif back in 2010, when I independently had the same idea and wanted to write about it, but I don't think I made it public. Probably the idea is older. The reason I didn't write about it was that I was more attracted* to another solution I found, which led to an analytic extension of the black hole spacetime, and has Cauchy hypersurfaces but no discontinuities. I reproduce a picture of the Penrose diagram from an older post in which I say more about this:
A. The standard Penrose diagram of an evaporating black hole.
B The diagram from the analytic solution I proposed.
___________________________
* The reason I preferred to work at the second solution is that it allows the information to become available after the evaporation to an external observer. The solution which relies on completing the Cauchy hypersurface with a part inside the black hole doesn't restore information and unitarity for an external observer. I don't know if this is a problem, but many physicists believe that information should be restored for an external observer, because otherwise we would observe violations of unitarity even in the most mundane cases, considering that micro black holes form and evaporate at very high energies. I don't think this argument, also given by Sabine, is very good, because there is no reason to believe that micro black holes form at high energy under normal conditions. People arrive at high energies for normal situations because they use perturbative expansions, but this is just a method of approximation. And even so, I doubt anyone who sums over Feynman diagrams includes black holes. But nevertheless, I wouldn't like information to be lost for an outside observer after evaporation, but this is just personal taste, I don't claim that there is some experiment that proved this. And the solution I preferred to research allows recovery of information and unitarity for an external observer, and other things which I explained in the mentioned posts and my PhD thesis.
Friday, March 10, 2017
The Tablet of the Metalaw
This edition of the FQXi essay contest is called
Wandering Towards a Goal. My entry is called The Tablet of the Metalaw. This is the abstract:
Reality presents to us in multiple forms, as a multiple level pyramid. Physics is the foundation, and should be made as solid and complete as possible. Suppose we will find the unified theory of the fundamental physical laws. Then what? Will we be able to deduce the higher levels, or they have their own life, not completely depending on the foundations? At the higher levels arise goals, life, and even consciousness, which seem to be more than mere constructs of the fundamental constituents. Are all these high level structures completely reducible to the basis, or by contrary, they also affect the lower levels? Are mathematics and logic enough to solve these puzzles? Are there questions objective science can't even define rigorously? Why is there something rather than nothing? What is the world made of?
At this time (2017-03-11 08.59 AM ET) my essay is in the top position, so I will immortalize this ephemeral moment in the picture below, since I expect the order will change dramatically, given that the votes will continue for nearly a month, and then the FQXi panel will add their choices:
Wednesday, February 15, 2017
The Standard Model Algebra
arXiv link: https://arxiv.org/abs/1702.04336
A simple geometric algebra is shown to contain automatically the leptons and
quarks of a generation of the Standard Model, and the electroweak and color
gauge symmetries. The algebra is just the Clifford algebra of a complex
six-dimensional vector space endowed with a preferred Witt decomposition, and
it is already implicitly present in the mathematical structure of the Standard
Model. The minimal left ideals determined by the Witt decomposition correspond
naturally pairs of leptons or quarks whose left chiral components interact
weakly. The Dirac algebra is a distinguished subalgebra acting on the ideals
representing leptons and quarks. The resulting representations on the ideals
are invariant to the electromagnetic and color symmetries, which are generated
by the bivectors of the algebra. The electroweak symmetry is also present, and
it is already broken by the geometry of the algebra. The model predicts a bare
Weinberg angle θW given by sin2(θW)=0.25.
Subscribe to:
Posts (Atom)