Smooth Quantum Mechanics
Quantum Mechanics without discontinuities in time evolution
Abstract
I show that the apparent wave function collapse can take place smoothly, without discontinuities. The projections on the observable's eigenspaces can be obtained by delayed initial conditions, imposed to the smooth time evolution of the observed system entangled with the measurement device used for the preparation. Since the quantum state of this device is not entirely available to the observer, its unknown degrees of freedom inject, by the means of entanglement, an apparent randomness in the observed system, leading to a probabilistic behavior. By using this mechanism, we can construct a Smooth Quantum Mechanics (SQM), without the need of discontinuities in time evolution. Therefore, the probabilities occur because not all the involved systems have determined quantum states. The evolution is deterministic, but for an observer who has access only to an incomplete set of initial conditions, it appears to be indeterministic.
The problem of discontinuities in Quantum Mechanics
The time evolution of a Quantum System
A quantum system which is in a pure state, and not entangled with another system, evolves according to the Schrödinger equation:
$$\Bigg\{
\begin{array}{ll}
i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle=H(t)|\psi(t)\rangle \\
|\psi(t_0)\rangle=|\psi_0\rangle,
\end{array}
$$
where $|\psi(t)\rangle\in\mathcal{S}$ is a state vector from the state space $\mathcal{S}$, and $H(t)$ is the Hamiltonian, usually a hermitian operator on $\mathcal{S}$. If the quantum system is closed, then $H$ is time independent, but in general, it is time dependent, because of the interactions with other systems. For more general interactions, the observed system can become entangled with other systems, and its state will no longer be pure. In this case, as well as in the case when we don't know the initial data, but rather a probability distribution, we represent the state by a density operator $\rho$ on $\mathcal{S}$. For these situations we will employ, instead of the
Schrödinger's equation, the Liouville - von Neumann equation:
$$\Bigg\{
\begin{array}{ll}
i\hbar\frac{\partial\rho(t)}{\partial t}=[H(t),\rho(t)] \\
\rho(t_0)=\rho_0.
\end{array}
$$
The measurement problem
When a measurement is performed to a quantum system, the system is found to be in an eigenstate of the observable. There are two main problems raised by this fact. First: why only eigenstates of the observables are obtained as outcomes of the observations? Why don't we observe superpositions of such eigenstates, like a $|\textrm{dead}\rangle+|\textrm{alive}\rangle$ Schrödinger cat? This is the main problem of the measurement, which, in this article, will be accepted as it is, without offering an explanation. The second problem is the following. Knowing the state of a quantum system, and assuming that a measurement will find the system in an eigenstate of the observable, it seems like a discontinuous jump happens. How is this happening? Is this jump really discontinuous? What is its nature? In this article, I propose a solution to this discontinuity problem in Quantum Mechanics.
One-measurement
The
Schrödinger's equation, as well as the
Liouville - von Neumann equation, are PDE equations. Each solution can be uniquely specified by an initial condition. The initial condition is obtained by performing a measurement at an initial moment $t_0$.
Let's consider that we measure the polarization of a photon, at the instant $t_0$. The obtained result will determine the photon's polarization both for moments $t$ with $t$<$t_0$, and with $t>t_0$. The last statement needs some argumentation. A measurement is in general required to produce a minimal disturbance of the system; it is required to determine the system's state, and to let the system in the state it was found. At the quantum level, this is sometimes difficult. The outcome of a measurement depends on the observable we choose to measure. For example, by choosing a direction along which we measure the spin of an electron, we determine only two possible eigenstates, out of an infinity. In the case of the photon, we can impose the left or right circular polarization with the help of a wave plate. This is an initial condition imposed to the photon. Consider a pair of entangled photons, being obtained from a parametric down conversion, such that they have linear polarizations along directions which are orthogonal to each other. A polarization imposed to one of them, applies also to the other one. This mechanism is used in the delayed choice quantum eraser experiment [
SMKYKS00]. In this experiment, the polarization of one photon determines if we have interference or not. We can choose the polarization by imposing to the other photon a polarization, and we can do this after the other photon hit the screen. The polarization imposed to one of the two photons, is revealed to apply in past, until the pair of the two photons has been emitted, so that the second photon has the correct polarization. This shows that we can impose a polarization at $t_0$, which applies for instants of time before and after $t_0$.
The classical view is that the measurement only revealed the state of the system, and the solution of the evolution equation preexisted to the measurement. On the other hand, in Quantum Mechanics, we can choose what observable to measure, thus, we can choose the set of admitted eigenstates. So, if the solution we detected by measurement preexisted, it did this in a way that anticipated our choice of the observables. This choice can be performed with a delay, to make sure that it doesn't affect in a causal way the observed system. This was emphasized by Wheeler [
Whe77,
Whe78,
WZ83] when he revived (It seems that similar suggestions were made before by Weiszäcker [
Wei31] and Bohr [
Sch49].) the idea of delayed-choice experiments. In the case of the electron spin, when we choose the direction to measure the spin, we let available only two possible eigenstates for the spin. Had we choose a different direction, the eigenstates would be different. So, our choice limited the possible outcomes. And when we measure the spin, we determine not only what spin the electron has at $t_0$, but also for previous $t$, as we can see from entanglement situations like the one pointed by Einstein, Podolsky, and Rosen [
EPR35] (in Bohm's version [
Bohm51]).
We can conclude that one measurement determines uniquely the state at $t_0$, hence the solution, and this determination seems to affect the past in a weird way. We cannot say that it can change it, rather it is only an initial condition, established with a (very large) delay. Two measurements of the same system may be incompatible, and require something that looks like a wavefunction collapse. In the case of only one measurement (or when the measurement is the first one), the state prior to the measurement is not sustained by any data, so we can not talk about collapse. The one-measurement situation makes apparent that the eigenstate can be selected without involving the discontinuous wave function collapse. Two initial conditions may be incompatible, but only one cannot be, since it is the only condition. If after the first measurement we perform another, the things become more difficult, but the solution is similar, as we will see next.
Two-measurements case and the wave function collapse
Let's consider a system whose evolution is described by the
Schrödinger's equation. Suppose that, after an observation at $t_0$ finds the system in an eigenstate, we perform a second observation, at the time $t_1$. If the state predicted by the evolution equation is an eigenstate of the second observable, then it will be obtained at the second measurement. If not, then the second observation cannot impose an initial condition at $t_1$, compatible with the unitary evolution governed by the Schrödinger equation.
We can see that one observation imposes an initial condition to the Schrödinger equation, choosing a solution, but a second observation either confirms the solution, or it is incompatible with it. In this case, it should not be possible to perform more than one observation of a system.
A quantum system has a
wave-like behavior, described by the Schrödinger equation, or by the Liouville - von Neumann equation, and a
quantum behavior, expressed by the condition to be found in an eigenstate of the observable. These two behaviors seem to be incompatible.
But we know from experience that we can perform more observations to the same quantum system. This has the appearance of a jumping from one solution of the Schrödinger equation to another one, in a discontinuous fashion.
The analysis of delayed-choice experiments suggests that, if a collapse happened, it took place in advance, during the previous interaction, possible even at $t_0$ (please refer to
figure 1).
 Figure 1
Figure 1 In a delayed-choice experiment, the reduction seems to take place in advance, anticipating the experimenter's choice of the observable.
Why discontinuities cause problems?
The acceptance that a quantum system is subject of a discontinuous wave function collapse can raise several problems. On the one hand, if we consider the observed system as being a part of a larger one (perhaps the Universe), containing the measurement device too, as a quantum subsystem, the measurement can be described by the evolution equation, and we expect that no discontinuous collapse appears. But, when we refer to the observed system only, we cannot see how the discontinuity can be avoided. We seem to have a paradox: a system evolving with discontinuities, being in the same time a subsystem of one evolving smoothly.
Another problem is that the discontinuous collapse has been postulated, but never observed directly. We don't know of any mechanism which can produce it, and we don't know when exactly it takes place. An explanation is required, since we cannot accept that it simply happens.
In Quantum Mechanics, an observable that commutes with the Hamiltonian of the system is conserved during the evolution.
But the conservation holds only as long as the system evolves governed by the Hamiltonian (Schrödinger equation or Liouville - von Neumann equation).
Since performing a measurement makes the system jump in a totally different state, it is expected that the conservation laws are broken. For example, if we measure the momentum of the system, and then measure its position, then the initial momentum is lost. If we measure again the momentum, we should expect to obtain a totally different value than the first time. We can expect that, after several measurements, the conserved quantities of the system be totally blown up.
The discontinuities are incompatible with the conservation laws, but the conservation laws don't break down as a result of measurements. Something happens always to restore them.
To make them compatible, we need to appeal to a "magical postulate":
During the state vector reductions, the conservation laws can no longer be deduced from the Hamiltonian, but they must be restored in some way or another.
The problem is that we don't know any explanation for the conservation laws, other than the time evolution described by the
Schrödinger's equation and
Liouville - von Neumann equation. Breaking this evolution should break the conservation laws, contrary to our experimental observations.
The quantum world is like a great illusionist, who has in his sleeves a lot of tricks that make us believing that the quantum system jumps discontinuously from time to time. But we have to remember that, in the end, there must be a logical explanation for the illusion number presented in the show, and to look for the strings.
Can discontinuities be avoided?
In the following, I will show that the apparent wave function collapse can be explained by the standard Quantum Mechanics, minus the discontinuity, as a smooth and natural phenomenon. The first ingredient comes from the discussion above, concerning a system undergoing only one measurement. A measurement fixes the initial data for a quantum system; going to a larger system, makes those initial conditions insufficient, therefore, a new measurement is allowed. The second ingredient is the entanglement with the device performing the previous measurement (which will be named
preparation device).
Quantum Mechanics without discontinuities
We begin by considering the measurement from a semi-classical viewpoint: the observed system is quantum, and the preparation device is classical.
The semi-classical interaction approach
Let's consider a quantum system evolving according to the
Schrödinger's equation, subject to a first measurement (the preparation) starting at the instant $t_0$ and ending at $t_0+\varepsilon$, and a second measurement at $t_1>t_0+\varepsilon$. If we consider the preparation device as being classical, its influence can be described by an interaction Hamiltonian $H_{\textrm{int}}(t)$. Thus, in the Dirac picture, the Hamiltonian is:
$$H(t)=H_0+H_{\textrm{int}}(t).
$$
The preparation device is considered classical, this meaning that its true state, which is quantum, is unknown. There will be a large set of quantum states which, at the classical level, will look identical. This set of equivalent quantum states can be parameterized, with both discrete and continuous parameters. Let's take a smooth parameterization $u(t)$ of its continuous degrees of freedom. The interaction Hamiltonian $H_{\textrm{int}}(t)$ will depend on $u(t)$, such that $H_{\textrm{int}}(t)=H_{\textrm{int}}(t,u)$.
Each choice of the parameters $u(t)$ will lead to a state of the system at $t$ given by
$$|\psi(t,u)\rangle=U(t,t_0,u)|\psi(t_0)\rangle.
$$
Before the introduction of the degrees of freedom parameterized by $u(t)$, there was only one possible state at $t_1$ for the observed system. Now, by varying $u$, $|\psi(t_1,u)\rangle$ also changes.
We ask the following question:
What condition should the parameters $u$ satisfy, such that all possible outcomes of any possible observation taking place at $t_1$ are reached by $|\psi(t_1,u)\rangle$?
This is a problem of Quantum Control Theory. Under some general assumptions on $u(t)$, the condition is that the Lie group associated to the Lie algebra generated by the matrices of the form $iH(t,u)$ should contain all the possible unitary transformations. If the dimension of $\mathcal{S}$ is $n<\infty$, then it is enough that the rank of the Lie algebra generated in this way to be identical to the rank of the unitary Lie algebra $\mathfrak u(n)$. This holds when there is no time limit, but in our case, the time is limited to $t_0+\varepsilon$, bringing a new restriction. On the other hand, the Born rule assigns zero probability to projections on an orthogonal state. Therefore, we don't need to obtain at $t_1$ states orthogonal to $|\psi_0\rangle$.
The parameters $u(t)$ can be determined by appropriate initial conditions. Similarly to the one-measurement case, the initial conditions are determined such that the system evolves to be the appropriate eigenstate of the observable, at $t_1$.
In the
figure 2 we can see how the Hamiltonian can prepare the observed system to be in an eigenstate of the observable.
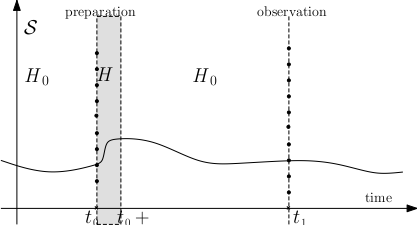 Figure 2
Figure 2 The disturbance in the evolution of the quantum system, introduced by the measurement device performing the preparation, needs to be taken into account by modifying the Hamiltonian from $H_0$ to $H(t,u)=H_0+H_{\textrm{int}}(t,u)$ for the time interval $(t_0, t_0+\varepsilon)$. This will "repair" the discontinuity presented in the
figure 1.
Assuming that the observable corresponding to the measurement at $t_1$ is $O_1$, for each outcome $|\psi_{O_1,\lambda}\rangle$ of the measurement, corresponding to an eigenvalue $\lambda$, there must exist a choice $u_{O_1,\lambda}$ of the parameters $u(t)$ such that the interaction send the observed system in $|\psi_{O_1,\lambda}\rangle$. The corresponding unitary operator is $U_{O_1,\lambda}(t_1,t_0)$, so that $|\psi_{O_1,\lambda}\rangle =U_{O_1,\lambda}(t_1,t_0)|\psi_0\rangle$.
Let us consider the following example, raised by Einstein to Bohr, at the Fifth Solvay Conference (Brussels 1927). Einstein said that, in a two-slit experiment, if we measure the recoil of the wall containing the two slits, when the light passes through it, one should be able to deduce whether the photon passed through one slit or the other. As Bohr replied to him, if we detect a significant recoil, the interference pattern is destroyed.
Let's reverse a bit the reasoning, and apply it to the delayed-choice [
Whe77,
Whe78,
WZ83,
Wei31,
Sch49] version of the two-slit experiment. We can decide after the photon has passed through the slit(s) whether to observe the "which way" or the "both ways" aspects. If we decide to observe the "which way" behavior, we cause the wall with the two slits to undergo a significant change of momentum (corresponding to the cases when the photon has passed through one slit or the other). If we choose to observe the interference, the change in momentum will be undefined. The wall with the two slits will get in a superposition of eigenstates of momenta.
This example shows that, indeed, the interaction with the wall with the two slits, happening in the interval $(t_0,t_0+\varepsilon)$, takes place in such a manner that the outcome of the measurement is one of those expected by the choice of the observable.
The entanglement approach
The previous analysis simplified the interaction between the preparation device and the observed system. A more general description will consider that the preparation device is quantum, not classical. In this case, its interaction with the observed system leads to an entanglement between the two. The evolution of the observed system can no longer be considered unitary: its state may go from being pure, at $t_0$, to being mixed at $t_0+\varepsilon$. Of course, the combined system made of the observed system and the preparation device, may be isolated, and undergo unitary evolution, but the observed system's state will be obtained by partial tracing the density operator of the larger system, and it will not necessarily be pure.
A correct description will use density operators to represent the state, and the
Liouville - von Neumann equation, for its evolution.
Let us consider that the state of the observed quantum system is described by the density operator $\rho_q$, on the state space $\mathcal{S}_q$, and the one of the preparation device is described by a density operator $\rho_p$ on the state space $\mathcal{S}_p$. We consider that the combined system, represented by a density operator $\rho_{q,p}$ on $\mathcal{S}_q\otimes \mathcal{S}_p$, is isolated. If it is not isolated, then we complete the system with remaining systems $\rho_r$, so that we obtain an isolated system. We can consider, without loosing the generality, that the preparation device incorporates all these systems, so it will be enough to work in the state space $\mathcal{S}_q\otimes \mathcal{S}_p$. The combined system will have a unitary evolution between $t_0$ and $t_0+\varepsilon$, given by the unitary operator $U_{q,p}=U_{q,p}(t_0+\varepsilon,t_0)$:
$$\rho_{q,p}(t_0+\varepsilon)=U_{q,p}\rho_{q,p}(t_0)U_{q,p}^\dagger
$$
The initial and the final density operators for the observed system can be obtained by partial trace:
$$\begin{array}{ll}
\rho_q(t_0)&=\textrm{tr}_p\rho_{q,p}(t_0)\\
\rho_q(t_0+\varepsilon)&=\textrm{tr}_p\rho_{q,p}(t_0+\varepsilon),
\end{array}
$$
and we have
$$\rho_q(t_0+\varepsilon)=tr_p(U_{q,p}\rho_{q,p}(t_0)U_{q,p}^\dagger).
$$
In general, the transformation from $\rho_q(t_0)$ to $\rho_q(t_0+\varepsilon)$ is not unitary.
We perform now another simplification, again without loosing generality, by purifying the state. We can purify the state $\rho_{q,p}$ by expanding the state space from $\mathcal{S}_q\otimes \mathcal{S}_p$ to
$$\mathcal{S}:=\mathcal{S}_q\otimes \mathcal{S}_p \otimes \mathcal{S}'_q\otimes \mathcal{S}'_p,
$$
with $\mathcal{S}_q\cong \mathcal{S}'_q$ and $\mathcal{S}_p\cong \mathcal{S}'_p$. The two extra state spaces $\mathcal{S}'_q$ and $\mathcal{S}'_p$ does not necessarily represent physical systems, but they allow us to consider $\rho_{q,p}$ as the partial trace of a pure state on $\mathcal{S}$. The composed system's evolution can be considered to be described by
Schrödinger's equation on $\mathcal{S}$, although the state $\rho_{q,p}$ still needs to obey
Liouville - von Neumann equation.
We denote the state space which is external to our observed system by
$$\mathcal{S}_e:=\mathcal{S}_p \otimes \mathcal{S}'_q\otimes \mathcal{S}'_p,
$$
and the density operator describing the evolution on this space by $\rho_e$.
The conditions imposed by the observations to the system described by $\rho_q$ at $t_0$ and $t_1$ imply that $\rho_q(t_0)$ and $\rho_q(t_1)$ represent pure states:
$$\begin{array}{l}
\rho_q(t_0)=|\psi_0\rangle\langle\psi_0|\textrm{ and} \\
\rho_q(t_1)=|\psi_1\rangle \langle\psi_1|.
\end{array}
$$
This imposes restrictions also on the combined system $\rho_{q,p}$. After $t_0$ the systems $\rho_q$ and $\rho_p$ become entangled, and the second observation disentangles them, and also imposes to $\rho_e$ a purity condition
$$\rho_e(t_1)=|\eta_1\rangle \langle\eta_1|,
$$
with $\eta_1\in\mathcal{S}_e$.
Since at $t_0$ the preparation device and the observed system were being separated, the preparation device was in a state $\rho_p(t_0)$, which can be obtained by partial tracing from a pure state $|\eta_0\rangle\in \mathcal{S}_e$. Although the state vector $|\eta_1\rangle$ is uniquely determined by the observation at $t_1$, it depends on $|\eta_0\rangle$. Because we don't know the value of $|\eta_0\rangle$, to each possible $|\eta_0\rangle$, and to each possible outcomes $|\psi_0\rangle$ and $|\psi_1\rangle$ of the two measurements, will correspond a unique $|\eta_1\rangle$. In order to clarify this correspondence, we need to study some properties of linear operators acting between tensor products of vector spaces.
Let $\mathcal{V}_A$, $\mathcal{V}_B$, $\mathcal{V}_C$ and $\mathcal{V}_D$ be four vector spaces over a field $\mathbb{K}$, $\mathbb{K}=\mathbb{R}$ or $\mathbb{K}=\mathbb{C}$, and let
$$T:\mathcal{V}_A\otimes\mathcal{V}_B\to\mathcal{V}_C\otimes\mathcal{V}_D
$$
be a $\mathbb{K}$-linear morphism of vector spaces. We are interested in identifying the possible separable vectors $|A\rangle \otimes|B\rangle \in\mathcal{V}_A\otimes\mathcal{V}_B$ and $|C\rangle \otimes|D\rangle \in\mathcal{V}_C\otimes\mathcal{V}_D$ such that:
$$T(|A\rangle \otimes|B\rangle )=|C\rangle \otimes|D\rangle .
$$
Proposition 1.
Let us consider $|A\rangle$ and $|C\rangle$ fixed. The set of vectors $|B\rangle \in\mathcal{V}_B$, and the set of vectors $|D\rangle \in\mathcal{V}_D$, satisfying the equation
above, form vector subspaces $\mathcal{V}_B^{AC}\leq\mathcal{V}_B$, respectively $\mathcal{V}_D^{AC}\leq\mathcal{V}_D$.
Proof:
If $|B'\rangle$ and $|B''\rangle$ are such that $T(|A\rangle \otimes|B'\rangle )=|C\rangle \otimes|D'\rangle$ and $T(|A\rangle \otimes|B''\rangle )=|C\rangle \otimes|D''\rangle$ for some $|D'\rangle$ and $|D''\rangle \in\mathcal{S}_D$, then for any $z',z''\in\mathbb{C}$,
$$T(|A\rangle \otimes(z'|B'\rangle +z''|B''\rangle ))=z'T(|A\rangle \otimes|B'\rangle )+z''T(|A\rangle \otimes|B''\rangle )=\\
z'|C\rangle \otimes|D'\rangle +z''|C\rangle \otimes|D''\rangle =|C\rangle \otimes(z'|D'\rangle +z''|D''\rangle ),
$$
therefore the solutions $|B\rangle \in\mathcal{V}_B$ form a vector subspace $\mathcal{V}_B^{AC}\leq\mathcal{V}_B$. Consequently, the solutions $|D\rangle \in\mathcal{V}_D$ form a vector subspace $\mathcal{V}_D^{AC}=T(\mathcal{V}_B^{AC})\leq\mathcal{V}_B$.
Remark 1.
Since we have $\mathcal{V}_C\otimes\mathcal{V}_D\cong\mathcal{V}_D\otimes\mathcal{V}_C$, it follows from
Proposition 1 that a similar result holds for $|A\rangle$ and $|D\rangle$ fixed.
Proposition 2.
If the space $\mathcal{V}_C$ has a scalar product $\langle \;|\;\rangle$, the linear operator
$$T_B^{AC}:=T|_{\mathcal{V}_B^{AC}}
$$
is given, for $|C\rangle \neq 0$, by
$$T_B^{AC}(|B\rangle )=\frac{\textrm{tr}_C(T(|A\rangle \otimes|B\rangle )\otimes\langle C|)}{\langle C|C\rangle}.
$$
Proof:
To remove the $|C\rangle$ part from $|C\rangle \otimes|D\rangle$, we tensor $|C\rangle \otimes|D\rangle$ with $\langle C|\in\mathcal{V}_C^*$, partial trace over $|C\rangle \langle C|$, and then divide by $||C\rangle |^2$.
\end{proof}
Remark 2.
If $T$ defined
above is isomorphism, then $T_B^{AC}$ is isomorphism onto its image.
We can now apply the previous results to a unitary operator $U$ acting on our space $\mathcal{S}_q\otimes\mathcal{S}_e$:
$$U:\mathcal{S}_q\otimes\mathcal{S}_e\to\mathcal{S}_q\otimes\mathcal{S}_e,
$$
and to the equation
$$U(|\psi_0\rangle\otimes|\eta_0\rangle)=|\psi_1\rangle \otimes|\eta_1\rangle,
$$
obtaining the following corollaries.
Corollary 1.
Let us consider $|\psi_0\rangle$ and $|\psi_1\rangle$ fixed. The set of vectors $|\eta_0\rangle\in\mathcal{S}_e$, and the set of vectors $|\eta_1\rangle \in\mathcal{S}_e$, satisfying the equation
above, form isomorphic vector subspaces $\mathcal{S}_{e0}^{\psi_0\psi_1}\leq\mathcal{S}_e$, respectively $\mathcal{S}_{e1}^{\psi_0\psi_1}\leq\mathcal{S}_e$.
Proof:
Follows immediately from Proposition 1. and Remark 2.
A measurement at $t_1$, although determines the observed state to be in $|\psi_1\rangle$, it does not necessarily determine completely the state $|\eta_1\rangle$ of the preparation device.
Corollary 2.
Let us consider $|\psi_0\rangle$ and $|\eta_1\rangle$ fixed. The set of vectors $|\eta_0\rangle\in\mathcal{S}_e$, and the set of vectors $|\psi_1\rangle \in\mathcal{S}_q$, satisfying the equation from Remark 2, form isomorphic vector subspaces $\mathcal{S}_{e0}^{\psi_0\eta_1}\leq\mathcal{S}_e$, respectively $\mathcal{S}_{q1}^{\psi_0\eta_1}\leq\mathcal{S}_q$.
Proof:
Follows from the Remark 1.
We denote the isomorphism obtained by restricting the unitary operator $U$ to $\mathcal{S}_{e0}^{\psi_0\eta_1}$ by $K_{\psi_0\eta_1}$.
From Corrolary 2 we obtain:
Theorem.
The set of all states $|\psi_1\rangle \in\mathcal{S}_q$ that can appear in the right side of the equation in Remark 2, for a fixed $|\psi_0\rangle\in\mathcal{S}_q$ is given by the following union of subspaces:
$$\mathcal{S}_{q1}^{\psi_0}:=\bigcup_{|\eta_1\rangle \in\mathcal{S}_e}\mathcal{S}_{q1}^{\psi_0\eta_1},
$$
obtained by varying the state vector $|\eta_0\rangle$ in the set
$$\mathcal{S}_{e0}^{\psi_0}:=\bigcup_{|\psi_1\rangle \in\mathcal{S}_q}\mathcal{S}_{e0}^{\psi_0\psi_1}.
$$
Remark:
A good preparation must satisfies the condition
$$\mathcal{S}_{q1}^{\psi_0} \geq \{|\psi_1\rangle \in\mathcal{S}_q|\langle\psi_1|U(t_1,t_0)|\psi_0\rangle\neq 0\},
$$
where $U(t_1,t_0)$ is the evolution operator of the observed system, if the system is undisturbed.
We recall that the state space $\mathcal{S}_e$ is an extension of a $\mathcal{S}_q$, made for working with purified states, but this is not a problem, since we can always recover the density operators of the subsystems by partial tracing.
The mechanism proposed here is represented in the
figure 3. The preparation should consist in an interaction with the property that any possible outcome $|\psi_1\rangle$ of the second measurement can be fitted by an appropriate choice of the initial conditions for the preparation device, represented by the state vector $|\eta_0\rangle$.
 Figure 3
Figure 3 Each possible outcome $|\psi_1^i\rangle$ can be obtained by choosing the appropriate states $|\eta_0^i\rangle$ representing the preparation device.
The smooth projection mechanism
Because the first measurement can find the observed system in the state $|\psi_0\rangle$, while the second one in $|\psi_1\rangle \neq U(t_1,t_0)|\psi_0\rangle$, it is easy to understand why it seemed that the state vector suffers a discontinuous jump, somewhere between $t_0$ and $t_1$. But we can now explain the wave function collapse as taking place smoothly, restoring the continuity in its evolution.
In order to do this, we had to go to the level of a larger system, composed by the observed system and the preparation device. At that level, the unitary evolution has been restored, and we have seen that the observed system (although its evolution may no longer be unitary, being entangled with the preparation device) can undergo a "smooth collapse".
The price to be paid was the acceptance that the observed system acts, somehow, anticipating the set of possible eigenstates. This feature may seem acausal, but it is present also in the standard Quantum Mechanics, as we have learned from the "delayed-choice experiments". In this article, the collapse was only pushed to the "beginning of times", and the initial conditions remained at the time $t_1$, being thus "delayed initial conditions".
Each measurement specifies the initial conditions of a system. When a system is measured a second time, the initial conditions need to be restated. To be restated without contradicting the previously observed initial conditions, they should be lost somehow. I hypothesized here that they are lost because of the interaction with the preparation device, which, although determines the previous set of conditions, transfers from its own indeterminacy of initial conditions to the observed system. Any interaction of a system with another system which has some freedom in the choice of its initial conditions, will make the former system loose its specification of the initial conditions. The observation only shows what the state was, and not what it will be at the next measurement.
Our mechanism allows us to see the projection, usually being associated to the wave function collapse, as taking place continuously, smoothly, and not discontinuously. The projector operator is not present explicitly in the evolution equation, but it is "embedded" in a set of operators parameterized by $|\eta_0\rangle$ - it can be reconstructed, for each pair $(|\psi_0\rangle,|\psi_1\rangle )$, by choosing an appropriate $|\eta_0\rangle\in\mathcal{S}_e$.
Discussion
Smooth Quantum Mechanics
Smoothness
This article provides a scenario of how the wave function collapse can take place without discontinuities, in a smooth way. We can reconstruct the Quantum Mechanics into a Smooth version, but we have to remember that this is not the only place where discontinuities occur. For example, the eigenstates of the position are distributions, and the eigenstates of the momentum have infinite norm. If we consider the state space as being a Hilbert space, then we have to accept such problems. Yet, we can avoid this kind of problems by renouncing at the completeness - the idea that the state space should contain limits for any Cauchy sequence. We can instead use a rigged Hilbert space, $\mathcal{S}\subset \mathcal{H}\cong\mathcal{H}^*\subseteq\mathcal{S}^*$. The state vectors will then be elements of a space $\mathcal{S}$ of smooth functions of finite norms, but the (ideal) eigenstates of various operators will belong to $\mathcal{H}$.
Probabilities
The evolution equations are deterministic, and since we have eliminated the discontinuities, the only source of randomness is in the initial conditions. Therefore, both the Born rule and the Heisenberg relations have to be reinterpreted. The Born rule doesn't expresses the probabilities of collapse, but those of the initial conditions to lead to each outcome.
We can derive the original Heisenberg relations [
WZ83] by multiplying the relations $\Delta\omega\Delta t\geq 2\pi$ and $\Delta k_x\Delta x\geq 2\pi$, from the Fourier analysis, with the reduced Plank constant $\hbar$.
To obtain similar Heisenberg relations for other pairs of conjugated operators, we do the same for the corresponding eigenbases.
These relations refer to how large the support of a state vector can be, when expressed in two different bases, and have nothing intrinsically probabilistic built in.
For example, the relation $\Delta k_x\Delta x\geq 2\pi$ shows that if the wave packet is too located in space, then in the momenta space it will be more spread.
We can obtain also the Heisenberg's relations from the commutation relations of the operators.
A version of Heisenberg's relations, which is used frequently, is $\sigma(p_x)\sigma(x)\geq \frac 1 2\hbar$, expressed in terms of the
standard deviation, defined for an operator $A$ by $\sigma(A):=\sqrt{\langle A^2\rangle-\langle A\rangle^2}$. Again, the probabilities have not yet entered into the play, because the standard deviations, in this case, refer to the components of the wave packet, expressed in two conjugate bases.
It is only when the state vector is disturbed by a preparation, and we apply the Born rules in relation to an eigenbasis of an observable, when Heisenberg's relations become the
uncertainty relations. It follows that the probabilistic meaning of the Heisenberg's relations also reflects our ignorance of the initial conditions.
The observers don't have access to the full set of initial conditions. The observations allows them collect only a set (which we will name
registry) of partial initial conditions. Therefore, although the evolution is deterministic, they perceive the time evolution as being indeterministic.
Causality and delayed initial conditions
The mechanism in Smooth Quantum Mechanics resumes to fixing the initial conditions at a moment of time, even for events prior to that moment. In fact, from mathematical point of view, the same solution of a PDE can be obtained from appropriate initial conditions imposed at any instant of time.
The main motivation for choosing the solution of delayed initial conditions resides in the avoidance of discontinuities. The discontinuities are source of problems. They imply that there are two sets of physical laws at quantum level. The discontinuities have never been observed directly, only the incompatibility between the outcomes of the measurements. They require additional explanations for the conservation laws, which are respected always, although only the smooth evolution leads to them, as they are obtained from commutation with the Hamiltonian (or by Noether's theorem). The price for avoiding the discontinuous collapse is to allow the initial data to be specified with a delay.
But we should clarify whether or not the mechanism of delayed initial conditions breaks down the causality. As already mentioned, each new condition should be chosen such that it is compatible with the already chosen conditions. It is even possible to choose two or more conditions at positions and moments which can be related only with signals traveling with velocity greater than that of the light. In this case, if we account for relativity, we can add the two conditions to the registry simultaneously, taking care not to violate the compatibility. In a deterministic world, with the initial data completely specified, there is no room for phenomena which contradict the initial data. Similarly, in the Smooth Quantum Mechanics, all the initial data is required to be compatible with the initial data already acquired. A similar apparent acausality, manifested by the anticipation of future initial conditions, is also present in experiments with photons having negative group velocity [
GSBKB06]. Consequently, the causal loops and breaking of causality are avoided.
What remains to be done
This article only shows that it is possible to have a smooth, instead of a discontinuous, wave function collapse, and shows that it is possible a smooth reconstruction of Quantum Mechanics. Not any interaction is able to provide the freedom in initial conditions required to solving this problem. Perhaps, this is why not any interaction is a measurement, but this point needs to be developed better. Ideally, we would have a precise mathematical description of a measurement, and a theorem showing that from this description, we obtain precisely the required range of outcomes at a second observation. Having a good definition of the measurement apparatus will allow us to predict, for example, which interactions qualify as measurements. Maybe, for this understanding, we will have to wait until more challenging parts of the Quantum Mechanics - the reconstruction of the classical world from the quantum world, and the explanation of why a measurement can obtain only eigenstates of the observable as outcomes - will receive better explanations. Another important progress would be a deduction of the Born rule. At the current moment, it seems that this rule is independent on the Smooth Quantum Mechanics' principles, but it would be desirable to have at least a good definition of a measurement which will lead easier to a smooth version of the Projection Postulate, including the Born rule.
Relations with other interpretations of Quantum Mechanics
After about eight decades of progresses in Quantum Mechanics, the discussions between Einstein and Bohr remain of actuality.
Although their views seemed incompatible one another, the Smooth Quantum Mechanics presented here is friendly with both of them. I don't say that, had they living today, they would say that they had in mind this solution, but I hope that this is at least a small step towards a reconciliation between their viewpoints. In a way, Bohr was right to say that "a phenomenon does not exist, until is observed" [
Bohr28,
WZ83], and Einstein was right to hope for a better, more complete, explanation of the quantum phenomena.
Perhaps, Schrödinger's ideas are most compatible with the SQM, since he disliked the discontinuous collapse, and believed in the physical reality of the wave functions. For example, he took the charge density in the electron's wave function literally, not as a probability distribution, and, according to SQM, he may be right.
The electron is the electron's wave function, since it is not a point, it is a wave, having different "shapes", depending on the measured observables.
The determinism is regained, since the evolution is again deterministic. The efforts of de Broglie, Vigier, culminating with David Bohm's causal or ontological interpretation of Quantum Mechanics [
Bohm52,
BH93], are theories whose purpose is to restore the determinism, the causality, and the reality and independence of the world. The price, as we now know, was the necessity to admit the nonlocality [
Bel64,
CHSH69,
CS78,
ADR82,
Asp99]. SQM provides a deterministic theory without extra "hidden variables", rather, it is based on
undetermined variables, or
undetermined initial data. Here, "to determine" has a passive meaning - "to measure/observe", and an active one - "to choose". The initial data is determined by measurements, but we can choose what to measure. We can look at the indeterministic QM as applying to open systems only, whose description can be completed to a deterministic image by accounting for the parameters "hidden" in the environment.
The indeterministic view is not completely lost, since what the observer has is the
registry, which is never a complete set of initial data. Each new measurement can bring new information, and the registry can be extended in different ways. We can interpret this in two ways. The first way is that the past is not established, and it is progressively created by each new choice of the observables, and, consequently, by each new outcome of the measurement. The second way to see the things is that all possible worlds exist, like a sheaf, and when we choose the observable we reduce the sheaf of worlds compatible with our registry. Each extension of the registry reduces this sheaf. Therefore, SQM is compatible with the Many Worlds Interpretation, with the amendment that each world is deterministic, and the only split is in the observer's registry, which can be completed in many ways. We can call this version of MWI the Many Registry Interpretation.
Perhaps one reason in the acceptance of a fundamentally indeterministic behavior in Quantum Mechanics was the belief that this is the only way to allow the existence of free-will [
CK06,
CK08]. The Smooth Quantum Mechanics offers an alternative, a deterministic view, which is still compatible with the free-will, at the same extent as the standard QM. We have the same freedom in choosing what observable to measure, influencing by this the initial conditions [
tH07], but in a smooth and deterministic manner.
Bibliography
[SMKYKS00]
R.Y.S.K. Scully, Marlan O.; Yoon-Ho Kim, Y. Shih, Physical Review Letters (84:
1-5) (2000).
arxiv:quant-ph/9903047
[Whe77]
J. Wheeler, in
Quantum Mechanics a Half Century Later (1977), pp. 1--18
[Whe78]
J.A. Wheeler, in
In A.R. Marlow, ed., Mathematical Foundations of Quantum Theory (1978), p. 30
[WZ83]
J.A. Wheeler, W.H. Zurek.
\newblock Quantum theory and measurement (1983)
[Wei31]
K.F. Weisz\"acker, Zeit. F. Phys. (70), 114 (1931)
[Sch49]
P.A.S. Ed.,
Albert Einstein : Philosopher-Scientist. The library of living philosophers, vol VII. (Cambridge University Press, 1949)
[EPR35]
A. Einstein, B. Podolsky, N. Rosen.
\newblock Can quantum-mechanical description of physical reality be considered
complete?, physical review 47:777--780 (1935)
[Bohm51]
D. Bohm, Quantum Th. pp. 611--623 (1951)
[GSBKB06]
G.M. Gehring, A. Schweinsberg, C. Barsi, N. Kostinski, R.W. Boyd, Science
(312), 895 (2006)
[Bohr28]
N. Bohr, Naturwissenschaften \textbf{16}, 245 (1928).
\newblock \doi{10.1007/BF01504968}
[Bohm52]
D. Bohm, Phys. Rev (85) (1952)
[BH93]
D. Bohm, B. Hiley.
\newblock The undivided universe: an ontological interpretation of quantum
mechanics. routledge and kegan (1993)
[Bel64]
J.S. Bell, (1964)
[CHSH69]
J.F. Clauser, M.A. Horne, A. Shimony, R.A. Holt, Physical Review Letters (23)
(1969)
[CS78]
J.F. Clauser, A. Shimony, in
Reports in the Progress of Physics (1978)
[ADR82]
A. Aspect, J. Dalibard, G. Roger, Physical Review Letters (49) (1982)
[Asp99]
A.B. Aspect.
\newblock Bell's inequality test: More ideal than ever. nature 398 (1999)
[CK06]
J. Conway, S. Kochen, Found. Phys. (36), 1441 (2006)
[CK08]
J. Conway, S. Kochen,
[tH07]
G. 't Hooft.
The free-will postulate in quantum mechanics (2007).
arxiv:quant-ph/0701097
 Introduction
Introduction Inscribing one regular polyhedron in another
Inscribing one regular polyhedron in another

 At a symmetry transformation, the vertex 1 can go in any of the four vertices. The vertices 2, 3 and 4 are all neighbor with the vertex 1, and they will remain so after the transformation too. Their order around the vertex 1 is preserved in the case of rotations, otherwise it is reverted. Therefore, the vertices’ permutation is even if and only if the transformation is a rotation. The regular tetrahedron having 24 automorphisms, they coincide with the elements of the group $S_4$. The rotations correspond to the elements of the alternating group $A_4$.
At a symmetry transformation, the vertex 1 can go in any of the four vertices. The vertices 2, 3 and 4 are all neighbor with the vertex 1, and they will remain so after the transformation too. Their order around the vertex 1 is preserved in the case of rotations, otherwise it is reverted. Therefore, the vertices’ permutation is even if and only if the transformation is a rotation. The regular tetrahedron having 24 automorphisms, they coincide with the elements of the group $S_4$. The rotations correspond to the elements of the alternating group $A_4$.

 For each edge of the dodecahedron, we take the four adjacent edges, and the other vertices of these edges form a square (hint: the four edges are diagonals in identical regular pentagons). These edges form five cubes. Each of the five cubes highlights six of the dodecahedron’s edges. It is easy to see that for each face we obtain a different ordering for the labels. Each rotation of the dodecahedron will take the face labeled by the ordered set (1, 2, 3, 4, 5) (we count starting with the vertex 1) in another face, also labeled with a permutation of the five numbers, so that 1 goes to one number, 2 to another etc. Thus, to the permutation (1, 2, 3, 4, 5) we can associate, as a result of the rotation, another permutation. Because we limit ourselves to rotations, we can choose one orientation (for example clockwise). The rotations will keep this orientation. Because we can start from any vertex of a face when we read the permutation, we will have five permutations for each face. This way, each corner of a face represents a permutation. We can check that these permutations are always even. Each dodecahedron’s rotation corresponds to an even permutation of the face labeled by (1, 2, 3, 4, 5). The dodecahedron’s rotations group is isomorphic with the alternating group $A_5$.
For each edge of the dodecahedron, we take the four adjacent edges, and the other vertices of these edges form a square (hint: the four edges are diagonals in identical regular pentagons). These edges form five cubes. Each of the five cubes highlights six of the dodecahedron’s edges. It is easy to see that for each face we obtain a different ordering for the labels. Each rotation of the dodecahedron will take the face labeled by the ordered set (1, 2, 3, 4, 5) (we count starting with the vertex 1) in another face, also labeled with a permutation of the five numbers, so that 1 goes to one number, 2 to another etc. Thus, to the permutation (1, 2, 3, 4, 5) we can associate, as a result of the rotation, another permutation. Because we limit ourselves to rotations, we can choose one orientation (for example clockwise). The rotations will keep this orientation. Because we can start from any vertex of a face when we read the permutation, we will have five permutations for each face. This way, each corner of a face represents a permutation. We can check that these permutations are always even. Each dodecahedron’s rotation corresponds to an even permutation of the face labeled by (1, 2, 3, 4, 5). The dodecahedron’s rotations group is isomorphic with the alternating group $A_5$.




 Calculator for the groups $C_n$ and $D_n$
Calculator for the groups $C_n$ and $D_n$ Polyhedral calculators of permutations
Polyhedral calculators of permutations Each face has four edges, and we label each of them, on that face, with the permutations obtained by reading the vertices’ labels, starting from that edge and walking clockwise. We obtain a cube labeled on each side of each edge with permutations. The reader can construct her own cube by printing this image:
Each face has four edges, and we label each of them, on that face, with the permutations obtained by reading the vertices’ labels, starting from that edge and walking clockwise. We obtain a cube labeled on each side of each edge with permutations. The reader can construct her own cube by printing this image: After assembling it in 3D, it will look like this:
After assembling it in 3D, it will look like this: For finding all the multiplications of the permutations from $S_4$ with a particular permutation, say (4132), we put the witness cube with the face containing the identical permutation (1234) in front, such that the identical permutation is below:
For finding all the multiplications of the permutations from $S_4$ with a particular permutation, say (4132), we put the witness cube with the face containing the identical permutation (1234) in front, such that the identical permutation is below: Then we put the resulting cube in a similar position, only that on the position of the identical permutation we put the permutation (4132):
Then we put the resulting cube in a similar position, only that on the position of the identical permutation we put the permutation (4132): Let’s suppose we want the result of the multiplication of the permutation (4132) with another permutation from $S_4$, for example (3124). We look in the witness cube the position of the permutation (3124), and in the result cube we read the permutation from the corresponding position. Because the permutation (3124) occurs in the witness cube on the left edge of the right face, we read the permutation from the left edge of the right face of the resulting cube. This is (3412).
Let’s suppose we want the result of the multiplication of the permutation (4132) with another permutation from $S_4$, for example (3124). We look in the witness cube the position of the permutation (3124), and in the result cube we read the permutation from the corresponding position. Because the permutation (3124) occurs in the witness cube on the left edge of the right face, we read the permutation from the left edge of the right face of the resulting cube. This is (3412).




