Round squares exist

Bertrand Russell said that there are no round squares. But there are. Here are two solutions.

A circle-square

This is a square that is circle:

To make it, first make a paper circle and  a paper square, with equal perimeters:

Fold them a bit:

Then glue their edges together:

The common boundary forms a square that is circle. It is a square, because in the blue surface it has right angles and equal straight edges. It is a circle, because in the red surface its points are at equal distance from a point. In fact, its points are at equal distance from the center even in space, because the red surface is ruled, and all the lines pass through the same point. So the common boundary is also a line on the surface of a sphere.

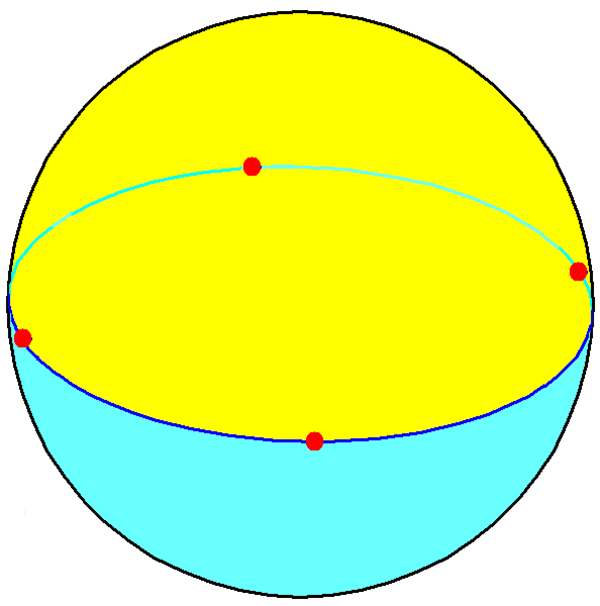
Round squares in non-Euclidean geometry

Consider for example the geometry on a sphere. On a sphere, polygons are made of the straightest lines on the sphere, which are arcs of the big circles. So, there are squares on a sphere

Image from Wikipedia

This is a square, since its edges are the shortest and straightest lines on the sphere, they have equal lengths, and its angles are all equal. If one gradually increases the size of the square, the angles increase too. At some point, the angles become $180^\circ$, and the edges become aligned, forming one single big circle:

Image from Wikipedia

So, is it a circle? Is it a square? It's a circle and a a square!